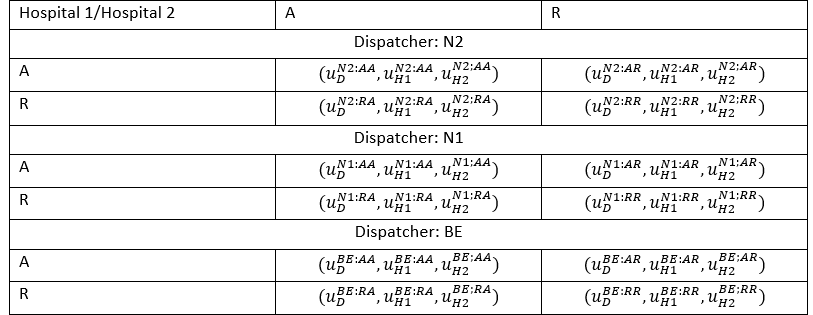
Dispatcher

Consider 1-D model with 2 hospitals, placed in opposite end of line. But now the decision about which hospital to take the patient to is taken by the new agent - dispatcher.

Dispatcher has 2 algorithm of patient distribution between hospitals:

• Deliver patient to closest hospital. If hospital has strategy 'R' and overcrowded, find next closest hospital.
• Deliver patient to hospital with best expected transporation and queue time

Dispatcher strategies are combinations of these algorithms:

• Strategy 'N2' - Nearest 2. Try to deliver to the nearest hospital, that can accept patient. Maximum number of iterations - 2. Then distribute patient using best expected time algorithm.
• Strategy 'N1' - Nearest 1. Try to deliver to the nearest hospital. Maximum number of iterations - 1. Then use best expected time algorithm.
• Strategy 'BE' - Best Expecation. Always use best expected time algorithm

With new agent, the decision on where to send patient can be independent of whether the hospital is ready to accept patient or not

Formulas

Hospital as before has 2 strategies:

• Accpet - always accept patient
• Reject - hospital can reject patient if it's overcrowded (has $N$ patients in queue)

Hospital with Accepting strategy has $M/M/c$ model.

Hospital with Rejecting strategy has $M/M/c/N$ model with a limited system capacity $N$.

But we will cosnider all hospitals as $M/M/c$ model (unlimited queue), because we will reject patients manually (to deliver patients to another hospital)

$ n $ is the number of parallel servers in hospital.

$\lambda$ is the request rate - mean value of arriving Poisson process

$\mu$ is the serving rate - mean time for serving process.

Total time is given by equation $ T = T_{transp} + T_{queue} + T_{surgery} $

$ t_c $ is time distance between to hospitals

$ \rho = \frac{\lambda}{\mu} $ - load parameter, the average number of requests arriving during serving a single request.

Probability of empty queue:

$$ P_0(\lambda) = [1+\sum_{j=1}^{n_i-1} \frac{\rho_i^j}{j!} + \frac{\rho_i^{n_i}}{(n_i - 1)! (n_i - \rho_i)}]^{-1} $$

Probability of k patients in queue:

$$ P_k(\lambda) = \frac{\rho_i^k}{k!} P_0 $$

Probability to reject patient:

$$ P_{rej}(\lambda) = 1 - P_0(\lambda) - \sum_{k=1}^{N_{lim}} P_k(\lambda) $$

Average number of patients in queue:

$$ L_Q(\lambda) = \frac{\rho_i^{n_i+1} \cdot n_i}{n_i! \cdot (n_i - \rho_i)^2} P_0(\lambda) $$

Average time in queue:

$$ W_Q(\lambda) = \frac{L_Q}{\lambda_e} $$

Average processing time:

$$ \widetilde{t}(\lambda) = W_Q(\lambda) + \frac{1}{\mu_i} $$

Dispatcher: N2 Strategy

Hospitals: AA strategy

$$ \lambda_i = \frac{\lambda}{2} $$ $$ T_i = \frac{t_c}{4} $$

Hospitals: AR/RA strategy

$\lambda_i^* = \lambda_j^* $ - source flow to hospital, before redirection

$ str[i] = R, str[j] = A $

$$ \lambda_i = \lambda_i^* \cdot (1 - P_{rej}(\lambda_i) $$

$$ \lambda_j = \lambda_j^* + \lambda_i \cdot P_{rej}(\lambda_i) $$

$$ T_i = \frac{t_c}{4} $$

$$ T_j = \frac{0.25 \lambda_j^* + 0.75 \lambda_i^* P_{rej}(\lambda_i^*)}{\lambda_j^* + \lambda_i^* P_{rej}(\lambda_i^*)} t_c = \frac{0.25 + 0.75 P_{rej}(\lambda_i^*)}{1 + P_{rej}(\lambda_i^*)} t_c $$

Hospitals: RR strategy

There are two flows of redirection - $ \lambda_{i, R1} = \lambda_i^* \cdot P_{rej}(\lambda_i), \quad \lambda_{i, R2} = \lambda_j^{R1} \cdot P_{rej}(\lambda_i^* + \lambda_j^{R1}) $

All patients from second flow of rejection will be distributed between hospitals by best expected travel and queue time.

$$ \lambda_{i,1} = \lambda_i^* - \lambda_i^{R1} $$

$$ \lambda_{i,2} = \lambda_j^{R1} - \lambda_i^{R2} $$

$$ \lambda_{i,12} = \lambda_{i,1} + \lambda_{i,2} $$

Now we need to distribute all patients, that has not been delivered to hospital after 2 rounds.

There are 2 flows - $\lambda_i^{R2}$ - patient that has been rejected at hospital j, and then at hospital i. And $\lambda_j^{R2}$ - opposite.

Distribution of patients by expected queue time depends on patients flow, but this distribution also changes flow, so we will define flow of patients, delivered to hospital by best expected time as recurrent formula.

At each step, we will add $\frac{\lambda_i^{R2}}{n}$ and $\frac{\lambda_j^{R2}}{n}$ flow to queue with less expected time.

Let $\lambda_i^{R2_j} $ - flow of patients from $\lambda_j^{R2}$, that delivered to hospital i, $\lambda_i^{R2_i} $ - flow of patients from $\lambda_i^{R2}$, that delivered to hospital i.

$$ \lambda_i^{R2_i}[0](n) = 0, \quad \lambda_i^{R2_j}[0](n) = 0 $$

$$ \lambda_i^{R2_i}[k](n) = \lambda_i^{R2_i}[k-1](n) + \frac{\lambda_i^{R2}}{n} [0.75 t_c + W_Q(\lambda_{i,12} + \lambda_i^{R2_i}[k-1](n) + \lambda_i^{R2_j}[k-1](n)) < 0.25 t_c + W_q(\lambda_{j,12} + \lambda_j^{R2_i}[k-1](n) + \lambda_j^{R2_j}[k-1](n)) $$

$$ \lambda_i^{R2_j}[k](n) = \lambda_i^{R2_j}[k-1](n) + \frac{\lambda_j^{R2}}{n} [0.25 t_c + W_Q(\lambda_{i,12} + \lambda_i^{R2_i}[k-1](n) + \lambda_i^{R2_j}[k-1](n)) < 0.75 t_c + W_q(\lambda_{j,12} + \lambda_j^{R2_i}[k-1](n) + \lambda_j^{R2_j}[k-1](n) $$

$$ \lambda_i^{R2_i} = \lim_{k \rightarrow \infty} \lambda_i^{R2_i}[k](k), \quad \lambda_i^{R2_j} = \lim_{k \rightarrow \infty} \lambda_i^{R2_j}[k](k) $$

$$ \lambda_i = \lambda_{i,12} + \lambda_i^{R2_i} + \lambda_i^{R2_j} $$

$$ T_i = \frac{0.25 (\lambda_{i,1} + \lambda_i^{R2_j}) + 0.75 (\lambda_{i,2} + \lambda_i^{R2_i})}{\lambda_i} $$

Dispatcher: N1 Strategy

Hospitals: AA, AR, RA strategy

Patient inflow will be the same, as in Dispatcher 'N2' strategy

Hospitals: RR strategy

The only change compared to Dispatcher 'N2' strategy will be that patients from R1 (insted of R2) will be distributed by best expected time algorithm

$$\lambda_{i,1} = \lambda_i^* - \lambda_i^{R1} $$

$$ \lambda_i^{R1_i}[0](n) = 0, \quad \lambda_i^{R1_j}[0](n) = 0 $$

$$ \lambda_i^{R1_i}[k](n) = \lambda_i^{R1_i}[k-1](n) + \frac{\lambda_i^{R1}}{n} [0.25 t_c + W_Q(\lambda_{i,1} + \lambda_i^{R1_i}[k-1](n) + \lambda_i^{R1_j}[k-1](n)) < 0.75 t_c + W_q(\lambda_{j,1} + \lambda_j^{R1_i}[k-1](n) + \lambda_j^{R1_j}[k-1](n)) $$

$$ \lambda_i^{R1_j}[k](n) = \lambda_i^{R1_j}[k-1](n) + \frac{\lambda_j^{R1}}{n} [0.75 t_c + W_Q(\lambda_{i,1} + \lambda_i^{R1_i}[k-1](n) + \lambda_i^{R1_j}[k-1](n)) < 0.25 t_c + W_q(\lambda_{j,1} + \lambda_j^{R1_i}[k-1](n) + \lambda_j^{R1_j}[k-1](n)) $$

$$ \lambda_i^{R1_i} = \lim_{k \rightarrow \infty} \lambda_i^{R1_i}[k](k), \quad \lambda_i^{R1_j} = \lim_{k \rightarrow \infty} \lambda_i^{R1_j}[k](k) $$

$$ \lambda_i = \lambda_{i,1} + \lambda_i^{R1_i} + \lambda_i^{R1_j} $$

$$ T_i = \frac{0.25 (\lambda_{i,1} + \lambda_i^{R1_i}) + 0.75 \lambda_i^{R1_j}}{\lambda_i} $$

Dispatcher: BE Strategy

When Dispatcher use 'BE' strategy - no matter what strategies hospitals will use.

Now we need to distribute all patients by best expected time algorithm

Let define $\lambda_i^i $ - pateints, located near hospital i, that will be delivered to hospital i, $ \lambda_i^j $ - patients, located near hospital j, that will be delivered to hospital j.

$$ \lambda_i^i[0](n) = 0, \quad \lambda_i^j[0](n) = 0 $$

$$ \lambda_i^i[k](n) = \lambda_i^i[k-1](n) + \frac{\lambda_i^*}{n} [0.25 t_c + W_Q(\lambda_i^i[k-1](n) + \lambda_i^j[k-1](n)) < 0.75 t_c + W_q(\lambda_j^i[k-1](n) + \lambda_j^j[k-1](n))] $$

$$ \lambda_i^j[k](n) = \lambda_i^j[k-1](n) + \frac{\lambda_j^*}{n} [0.75 t_c + W_Q(\lambda_i^i[k-1](n) + \lambda_i^j[k-1](n)) < 0.25 t_c + W_q(\lambda_j^i[k-1](n) + \lambda_j^j[k-1](n))] $$

$$ \lambda_i^i = \lim_{k \rightarrow \infty} \lambda_i^i[k](k), \quad \lambda_i^j = \lim_{k \rightarrow \infty} \lambda_i^j[k](k) $$

$$ \lambda_i = \lambda_i^i + \lambda_i^j $$

$$ T_i = \frac{0.25 \lambda_i^i + 0.75 \lambda_i^j}{\lambda_i} t_c $$

Game

We will define non-cooperative game for 3 players.

Utility function for hospitals: $$\frac{\lambda_i}{t_i}$$

Utility function for dispatcher - inverse global average time: $$\frac{\lambda_i + \lambda_j}{\lambda_i \cdot t_i + \lambda_j \cdot t_j} $$

To find optimal solution need to maximize both functions

As a result, game matrix will be the following.

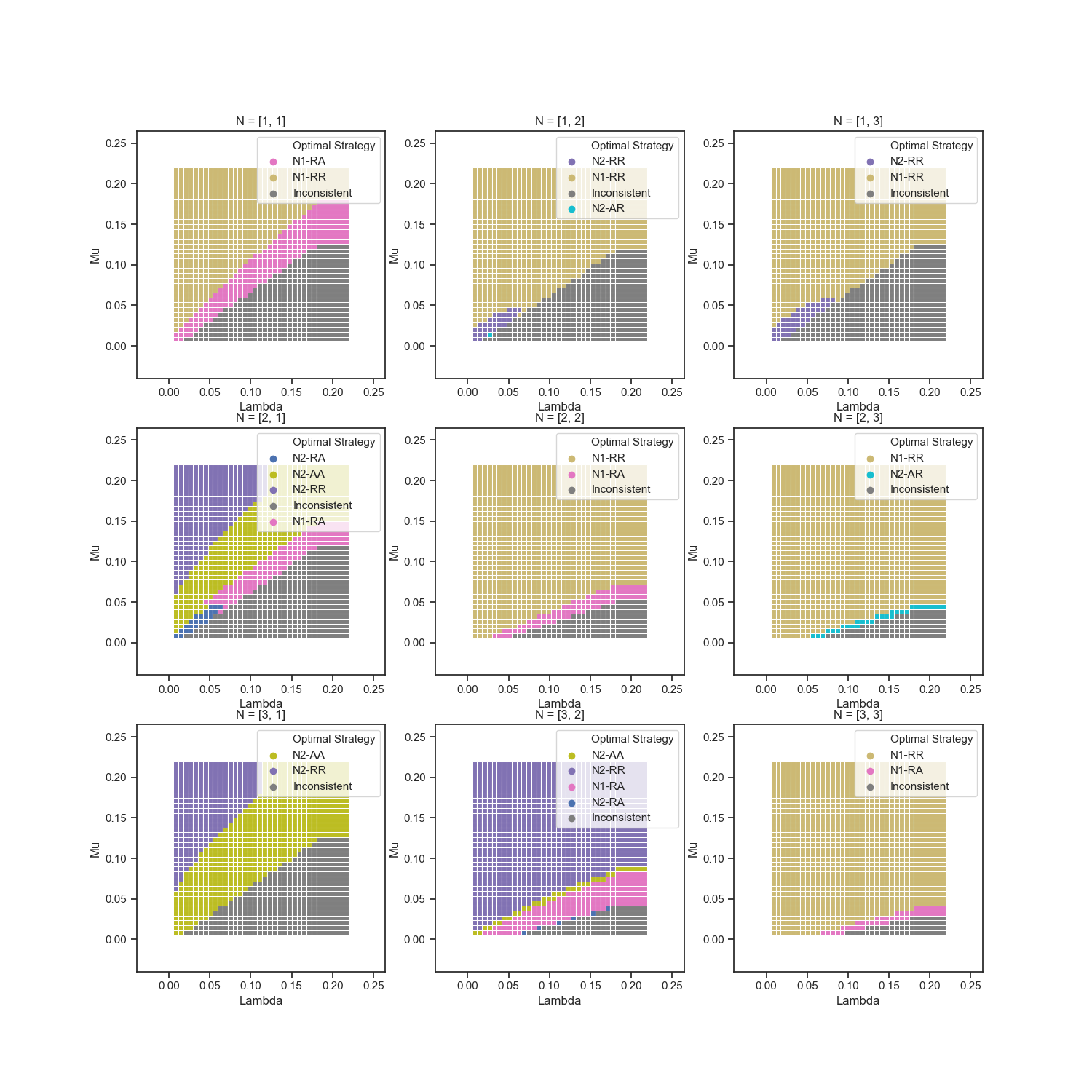
Nash Equilibrium

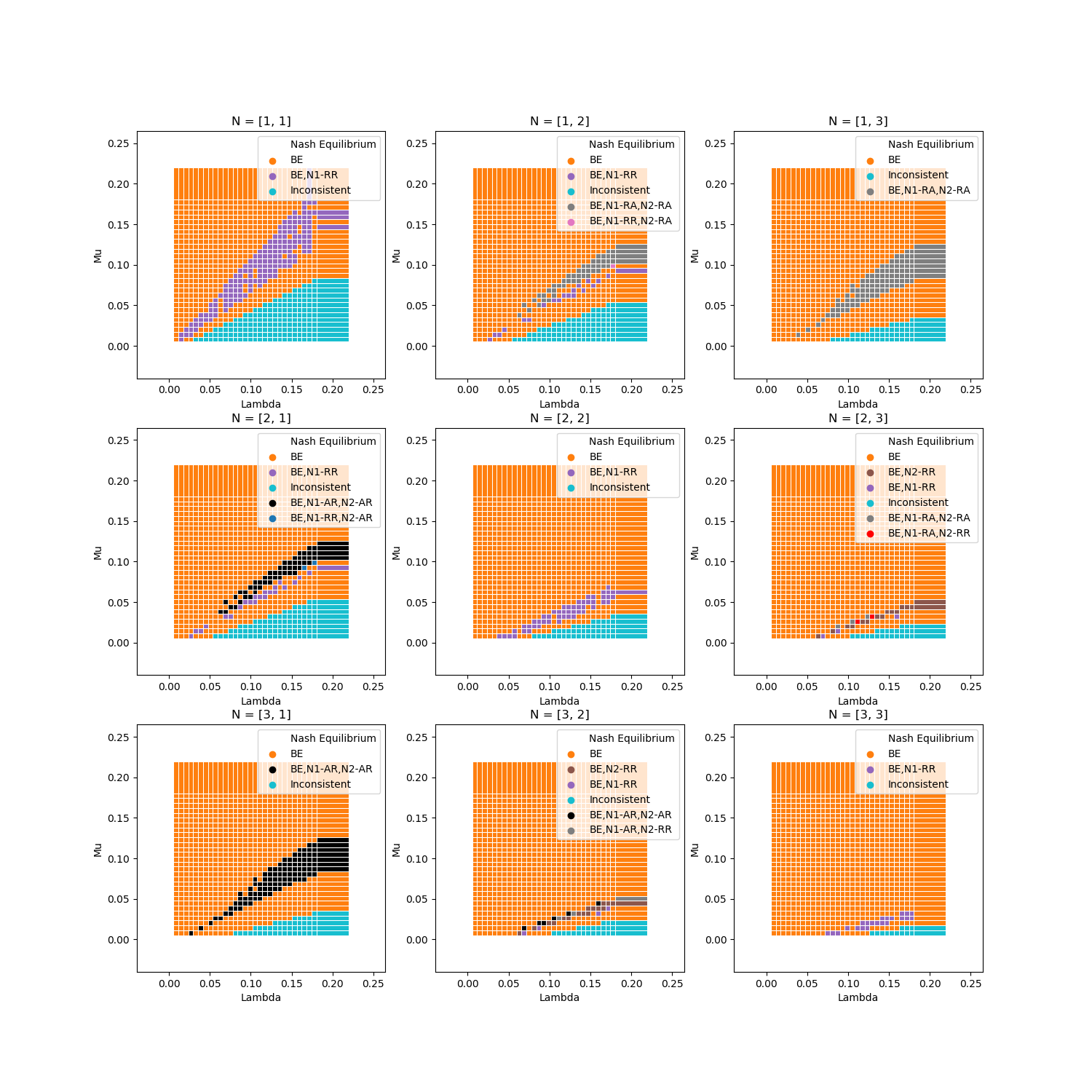
Dispatcher: {N2, N1} NashEquilibrium

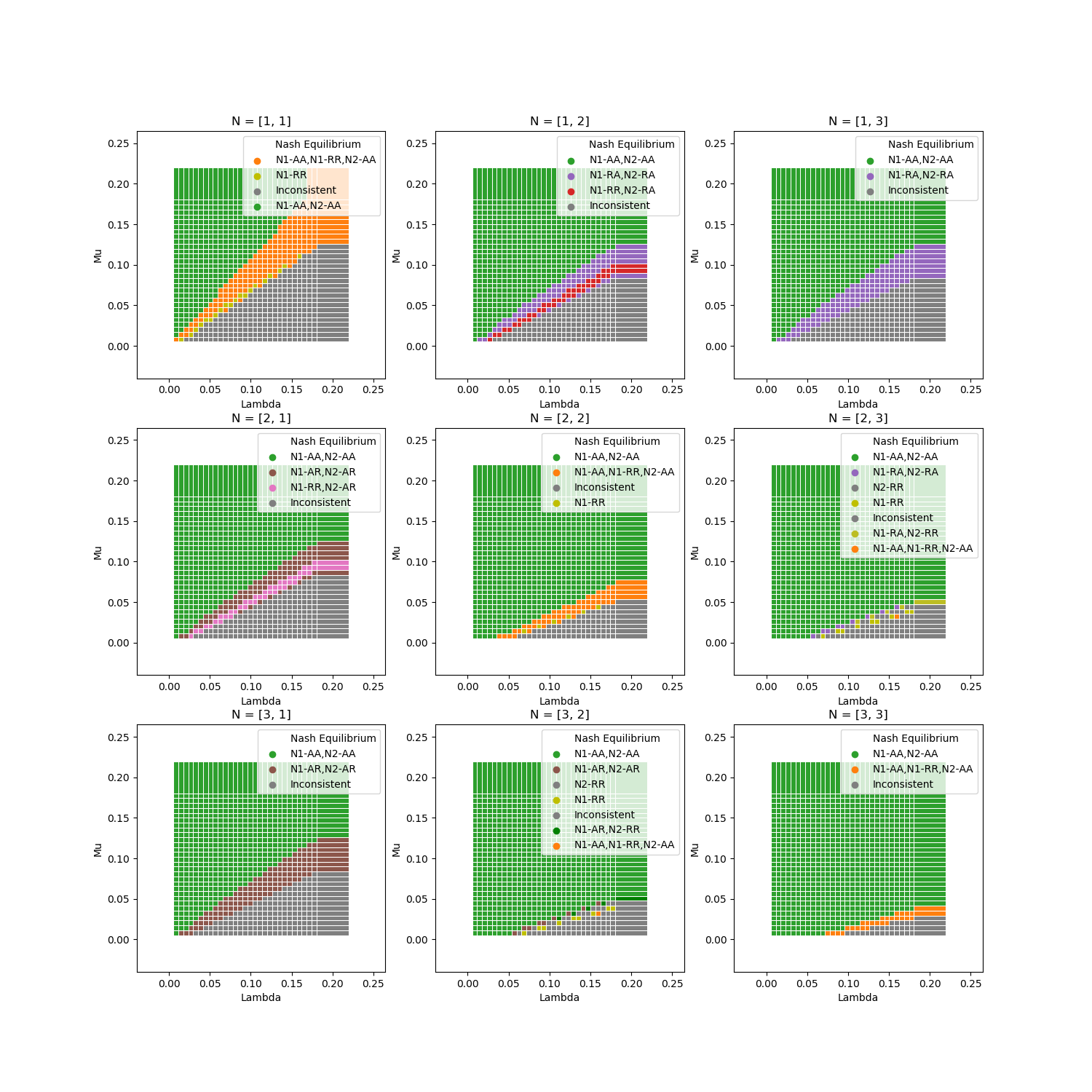
Patient Inflow: Global Time (need to minimize)

Global Time

N1;RR is optimal strategy for global time

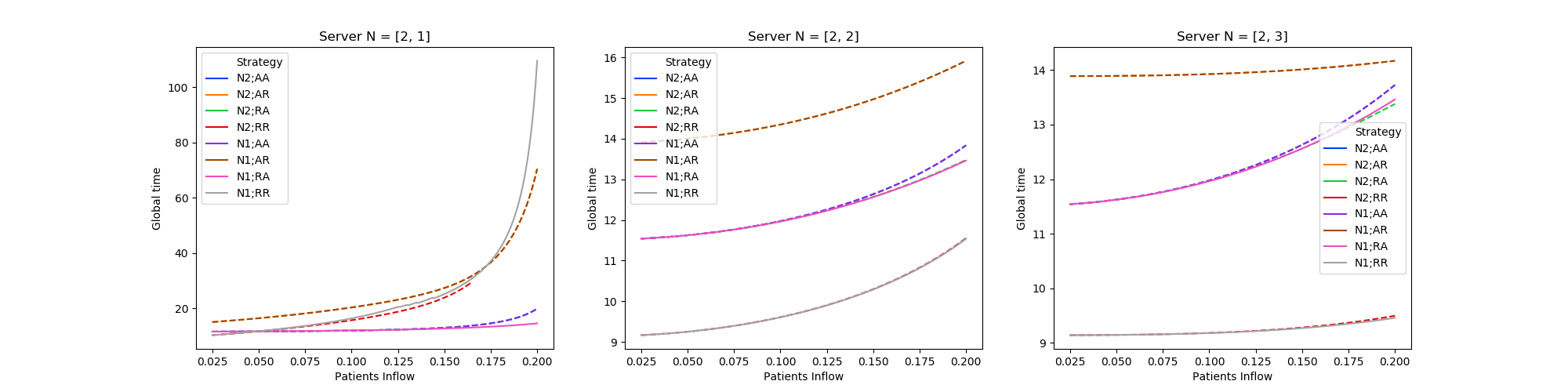
Mixed Strategies for 2 Hospitals

Mixed Strategies for 2 Hospitals with Dispatcher N2 Strategy

Mixed Strategies for 2 Hospitals with Dispatcher N1 Strategy